

I docenti del corso di laurea in Matematica propongono una serie di seminari scientifici per gli studenti delle scuole superiori, che hanno lo scopo di avvicinare i ragazzi al mondo della ricerca scientifica. Le attività, tutte di carattere divulgativo, consentiranno agli studenti di acquisire familiarità con alcuni aspetti meno consueti della matematica, sia teorica sia applicativa.
Presso le scuole che ne faranno richiesta, in presenza oppure col docente collegato da remoto.
Se non diversamente indicato, tutti i seminari sono della durata di circa un’ora. Le date saranno concordate fra il relatore e la scuola ospitante.
Per organizzare un seminario presso la propria scuola, contattare il Prof. M. Semplice.
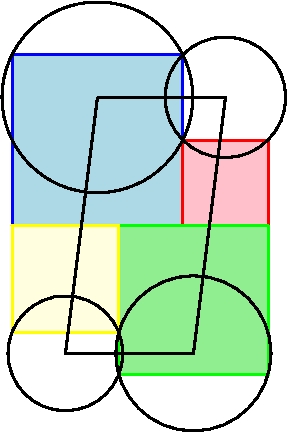
Molti oggetti geometrici come ad esempio la circonferenza e l'asse di un segmento, possono essere definiti attraverso il concetto di distanza. Questo concetto però può essere generalizzato e questo conduce a "strane" modificazioni delle figure geometriche che sembrano in palese contrasto con le forme a cui siamo abituati.
Accessibile a tutti gli studenti.
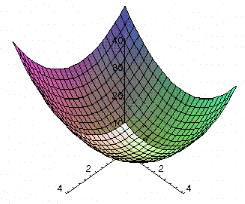
Scriveva Eulero:
Nulla accade nel mondo in cui non risplenda una qualche regola di massimo o di minimo
.
Discuteremo come nel mondo che ci circonda tra tutti i possibili eventi e negli
ambiti più diversi tra cui biologia, economia e ingegneria, si verifichino
quelli che rendono minima l'energia, un principio di “risparmio” che consente di
scrivere equazioni particolarmente significative e che allo stesso tempo è fonte
d'ispirazione per studiarle.
Accessibile a tutti gli studenti.

Quando si cerca un’informazione su Google assegnando parole chiave, si ottiene una lista di pagine web ordinata secondo un criterio di “importanza”. La nozione di “importanza” può essere formulata in linguaggio matematico, permettendo così l’utilizzo di metodi numerici per la determinazione dell’ordinamento delle pagine web trovate e la dimostrazione di esistenza e unicità di tale ordinamento. Introducendo mediante un semplice esempio il formalismo matematico che permette di rappresentare il web e il concetto di “importanza”, si descrive nel dettaglio il metodo numerico di base per l’ordinamento dei risultati di ricerca di Google. Data l'enorme quantità di dati, la comunità scientifica è continuamente alla ricerca di algoritmi sempre più efficienti e veloci. Questo permetterà di discutere l’importanza della complessità computazionale di un algoritmo e quindi del software rispetto all’hardware.
Accessibile a tutti gli studenti. (Possono essere utili vettori e matrici)
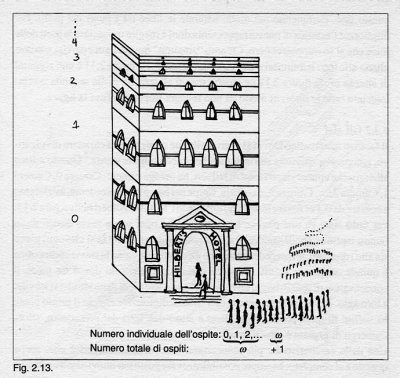
I concetti di più grande e più piccolo ai quali siamo abituati considerando
insiemi finiti di oggetti, e che si riassumono nel principio che la parte è
più piccola del tutto sembrano dare luogo a situazioni paradossali quando si
considerano insiemi infiniti, tanto che Galileo scriveva:
Io non veggo che ad altra decisione si possa venire, che a dire [...]
gli attributi di
uguale, maggiore e minore non aver luogo negli infiniti, ma solo nelle quantità
terminate
. Dopo aver discusso brevemente cosa significa contare il numero di
elementi di un insieme, descriveremo alcuni di questi paradossi, e vedremo come
opportunamente interpretati si possono inserire queste situazioni paradossali in
una teoria matematica coerente della cardinalità.
Accessibile a studenti del 3o anno o superiore. (Può essere utile il concetto di funzione)

Si studieranno le serie numeriche che formalizzano, mediante un procedimento di limite, l'operazione di somma di infiniti numeri. Dopo aver descritto i principali strumenti che permettono di stabilire se questa somma infinita dà luogo ad un numero finito, si vedranno applicazioni legate agli sviluppi decimali, binari o in base arbitraria di un numero, e si dimostrerà in forma matematica che Zenone sbagliava, e che Achille infatti raggiunge e supera la tartaruga. Altre applicazioni verranno presentate. Alcuni concetti verranno esemplificati mediante l'uso del calcolatore in laboratorio informatico.
Accessibile a studenti del 3o anno o superiore. (Può essere utile il concetto di limite)
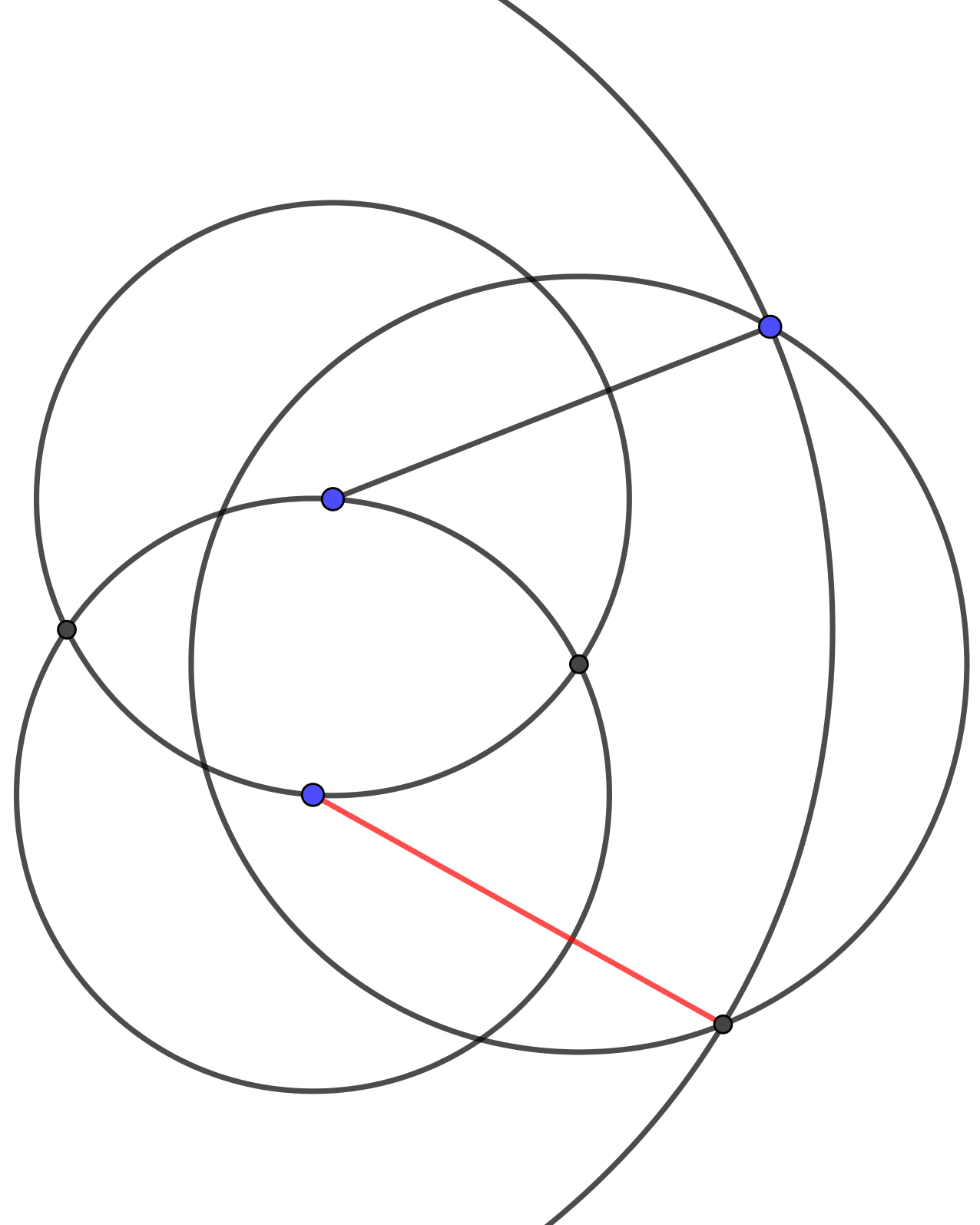
Le figure geometriche studiate da Euclide nei suoi Elementi sono tutte ottenibili a partire da figure elementari utilizzando solo riga e compasso. Gli antichi greci già sapevano come realizzare un gran numero di costruzioni: da quelle più semplici quale la costruzione del punto medio fra due punti, a quelle più elaborate quale la costruzione di un pentagono regolare a partire dal suo lato. I greci non furono però in grado di stabilire, ad esempio, se è possibile costruire un quadrato avente la stessa area di un cerchio dato o quali poligoni regolari possano essere costruiti a partire dal loro lato. Questi e altri problemi hanno avuto risposta solo 2000 anni dopo che sono stati posti, grazie ai risultati di Gauss, Wantzel, Lindemann e altri, mostrando che l'approccio giusto per affrontarli è di considerarli dal punto di vista algebrico. In particolare vedremo come la parola impossibile abbia, dal punto di vista matematico un significato diverso da quello talvolta usato nel linguaggio comune.
Fruibile da tutti gli studenti

Nel periodo in cui è ambientato il film «Il diritto di contare» i matematici, da veri e propri “calcolatori umani”, si sono trasformati in progettatori di algoritmi di calcolo. Ispirandoci ad alcune scene del film, illustriamo il ruolo fondamentale che i matematici hanno assunto nel calcolo scientifico moderno.
Accessibile a tutti gli studenti.\ È consigliato aver visto il film prima del seminario.

Partendo dal familiare esempio della geometria analitica, che ci permette di studiare le forme geometriche elementari utilizzando i metodi dell’algebra, presenteremo la nozione di “ponte” tra teorie matematiche differenti e daremo un’introduzione alle metodologie più recenti ed innovative che si possono utilizzare per mettere relazione tra loro teorie matematiche distinte e trasferire conoscenze tra di esse. Incontreremo in particolare il concetto di topos, che è in grado di incarnare la nozione di “contenuto” di una teoria matematica in maniera indipendente da come essa è “presentata” e illustreremo il ruolo di questi oggetti matematici nel servire da “ponti” per unificare tra loro teorie differenti.
Accessibile a tutti gli studenti.